Centered Kernel Alignment (CKA) in Detail

CKA is a state-of-the-art tool to measure the similarity of neural network representations, but in this post, I walk through its derivation in detail for a deeper understanding. [Original paper]

Oct 4, 2024 4 min read
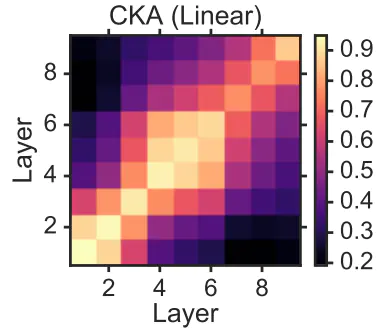CKA map example from original paper

1. Overview

CKA (Centered Kernel Alignment) is a state-of-the-art tool for measuring the similarity of neural network representations. It has practical uses such as comparing layers within a single model, comparing representations across two different architectures, or studying how representations evolve during training. After reading the original paper, I wanted more intuition about how the CKA formulae capture similarity, so I spent some time breaking it down. This post is a summary of my understanding of CKA and the derivations I worked out.

In summary, the key insight of CKA is the use of gram matrices that collapse the neuron dimension and instead compare inter-sample similarities, making the measure invariant to the width or bases of the layers being compared.

2. Inputs and Outputs

To run CKA, we must have 2 matrices of paired activations (aka representations) from the same neural network, or different neural networks.

Let’s call these matrices $X$ and $Y$. Let $X \in \mathbb{R}^{n \times d_1}$ and $Y \in \mathbb{R}^{n \times d_2}$, where $n$ is the number of samples and $d_i$ is the dimensionality of the representations. $d_1$ and $d_2$ can be different, but $n$ must be the same for both matrices as these represent paired samples. This means CKA lets us compare the similarity of representations that come from layers of differing widths. We also assume that these matrices have been centered, that is, the column means have been subtracted. Centering ensures the similarity measure is not skewed by constant offsets in activations, and is required for the HSIC connection discussed in Section 3.

3. Formula

One formula for (linear) CKA is given by: $$\text{CKA}(X,Y) = \frac{\lVert Y^TX \rVert_F^2}{\lVert X^TX \rVert_F \lVert Y^TY \rVert_F}$$

Let’s break down this equation:

  1. Breaking down the Numerator
    Let’s first look at the numerator of the formula: $$\lVert Y^TX \rVert_F^2$$ In Section 3 of Similarity of Neural Network Representations Revisited, we are shown a way to link from dot products between examples to dot products between features: $$ \lVert Y^TX \rVert_F^2 = \langle \text{vec}(XX^T), \text{vec}(YY^T)\rangle$$ This is the key insight of CKA, where a computation comparing the multivariate features between the two matrices can actually translate to computing the similarity between examples, and then comparing the resulting similarity structures. We will expand the formulation as follows in order to reach the intuition presented by the authors.

    We will work this the opposite way here, including more details to understand the intermediate steps. First, we will establish an important property of the Frobenius norm, and of the trace.

    1. frobenius norm reformulation: $\lVert A \rVert_F = \sqrt{\text{Tr}(A^TA)}$

    2. trace property (cyclic property): $\text{Tr}(ABC) = \text{Tr}(CAB) = \text{Tr}(BCA)$

    Now, we can rewrite the numerator of the CKA formula as follows:

$$ \begin{align*} \lVert Y^TX \rVert_F^2 &= \left(\sqrt{\text{Tr}((Y^TX)^T Y^TX)}\right)^2 && \text{frobenius norm}\\ &= \text{Tr}\left(X^TYY^TX\right) && \text{sqrt and transpose} \\ &= \text{Tr}\left(XX^TYY^T\right) && \text{cyclic trace} \\ &= \sum_i \left(XX^TYY^T\right)_{ii} && \text{expanding trace} \\ &= \sum_i \sum_j (XX^T)_{ij} (YY^T)_{ji} && \text{expanding matmul} \\ &= \sum_i \sum_j (XX^T)_{ij} (YY^T)_{ij} && \text{gram mats symm.} \\ &= \langle \text{vec}(XX^T), \text{vec}(YY^T)\rangle && \text{dot product def.} \end{align*} $$
Now we have a more complete understanding of the key Equation 1 in the paper, which relates feature similarity to the dot product between similarity structures.



  1. Connection to the Hilbert Schmidt Independence Criterion
    Before formulating the connection to the Hilbert-Schmidt Independence Criterion (HSIC), we’ll first recall the definition of the cross-covariance matrix $$\text{cov}(X,Y) = \frac{1}{n-1}\left(X - \mathbb{E}(X)\right)\left(Y - \mathbb{E}(Y)\right)^T$$ Now, we will connect the trace formulation from above to the covariance matrix. Remember that we assume our data matrices are already centered
$$\begin{align*} \lVert \text{cov}(X^T, Y^T)\rVert_F^2 &= \left\lVert \frac{1}{n-1} X^TY \right\rVert_F^2 && \text{by def. & center}\\ &= \frac{1}{(n-1)^2} \lVert Y^TX \rVert_F^2 && \text{scalar & norm} \\ &= \frac{1}{(n-1)^2} \text{Tr}\left(XX^TYY^T\right) && \text{from above} \end{align*}$$
The HSIC was originally proposed as a test statistic for determining if two variables are independent. The empirical estimator of HSIC, with kernels $K$ and $L$ and centering matrix $H_n = I_n - \frac{1}{n} \mathbb{1}\mathbb{1}^T$, is defined as: $$ \text{HSIC}(K,L) = \frac{1}{(n-1)^2} \text{Tr}(KHLH)$$

However, HSIC is not invariant to isotropic scaling — i.e., it does not satisfy $s(X,Y) = s(\alpha X, \beta Y)$ for a similarity index $s$. For CKA, we would like this property so that the score is not affected by the scale of the activations. Therefore, the authors propose a normalized version. We now derive the simplifications for both the linear kernel and the arbitrary kernel cases. For the linear kernel, we have: $$ \text{HSIC}(X,Y) = \frac{1}{(n-1)^2}\text{Tr}(X^TXY^TY) $$

For linear CKA, we get:

$$\begin{align*} \text{CKA}(X,Y) &= \frac{\text{HSIC}(K,L)}{\sqrt{\text{HSIC}(K,K)\text{HSIC}(L,L)}} \\ &= \frac{\frac{1}{(n-1)^2} \lVert Y^TX \rVert_F^2}{\sqrt{\frac{1}{(n-1)^2} \lVert X^TX \rVert_F^2 \frac{1}{(n-1)^2} \lVert Y^TY \rVert_F^2} }\\ &= \frac{\frac{1}{(n-1)^2} \lVert Y^TX \rVert_F^2}{\frac{1}{n-1}\cdot \frac{1}{n-1} \lVert X^TX \rVert_F \lVert Y^TY \rVert_F} \\ &= \frac{\lVert Y^TX \rVert_F^2}{\lVert X^TX \rVert_F \lVert Y^TY \rVert_F} \end{align*}$$

For an arbitrary kernel $K, L$, we simplify CKA as follows:

$$\begin{align*} \text{CKA}(K,L) &= \frac{\text{HSIC}(K,L)}{\sqrt{\text{HSIC}(K,K)\text{HSIC}(L,L)}} \\ &= \frac{\frac{1}{(n-1)^2} \text{Tr}(KHLH)}{\sqrt{\frac{1}{(n-1)^2}\text{Tr}(KHKH)\frac{1}{(n-1)^2}\text{Tr}(LHLH)}} \\ &= \frac{\text{Tr}(KHLH)}{\sqrt{\text{Tr}(KHKH)\text{Tr}(LHLH)}} \end{align*}$$

Together, these two formulations give a practical and kernel-flexible way to compare neural network representations, invariant to isotropic scaling and applicable across layers of any width.

Deep-Learning
Neha Verma
Neha Verma
PhD Student

I am a PhD student at Johns Hopkins Center for Language and Speech Processing.